Matrices especiales

Matriz Identidad

Llamamos matriz identidad a la matriz cuadrada (mismo número de filas que de columnas) formada por unos en la diagonal y ceros en las demás entradas (posiciones). La representamos por I_n donde n es la dimensión de la matriz.

 Propiedades:

• Es el neutro del producto de matrices. Es decir, para toda matriz A de dimensión m x n,
  
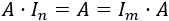
• Es idempotente, es decir, sus potencias son ella misma
  
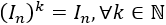
• Es regular y su inversa es ella misma.
• Es una matriz permutación.
• Sólo tiene un autovalor (valor propio), que es 1, con multiplicidad algebraica la misma que la dimensión de la matriz.

Notaciones habituales:

Matriz Diagonal

Todos los elementos son nulos excepto los de la diagonal, esto es, los elementos que tienen el mismo número de fila que de columna.
Una matriz A diagonal de dimensión m x n que tiene por elementos de la diagonal a los elementos del vector v se le denota por

 Propiedades:

• Son un caso particular de las matrices triangulares.
• La matriz traspuesta de una matriz diagonal de dimensión m x n es la matriz diagonal de dimensión n x m con la misma diagonal.
• En las matrices cuadradas, el determinante es el producto de los elementos de la diagonal:

 Con lo que son regulares si, y sólo si, todos los elementos de la diagonal son distintos de 0. En tal caso,

Potencias (para las cuadradas)

 Producto de matrices diagonales: Sean las matrices A y B diagonales de dimensiones respectivas m x n y n x t, su producto es una matriz diagonal de dimensión m x t

Los autovalores (valores propios) de las matrices diagonales cuadradas son los elementos de la diagonal.

Matriz Triangular

Distinguimos dos tipos:
triangular superior: todos los elementos por debajo de la diagonal de la matriz son 0, es decir,

triangular inferior: todos los elementos por arriba de la diagonal de la matriz son 0, es decir,

Propiedades de las matrices triangulares

• La matriz traspuesta de una triangular superior es triangular inferior y viceversa.
• Si la matriz es cuadrada, su determinante es el producto de los elementos de la diagonal

       

Por tanto, es regular si, y sólo si, los elementos de la diagonal son distintos de 0. En tal caso,

• La inversa de una matriz triangular superior (inferior) es una matriz triangular superior (inferior).
• El producto de matrices triangulares superiores (inferiores) es una matriz triangular superior (inferior).
• Los autovalores (valores propios) de una matriz cuadrada triangular son los elementos de la diagonal.

Matriz Traspuesta

La matriz traspuesta de una matriz A de dimensión m x n es una matriz de dimensión n x m que tiene por columnas a las filas de A. Se denota como A^T (o A' si la matriz es real).

Propiedades de la matriz traspuesta

• Traspuesta de la traspuesta:

• Traspuesta de la suma:

• Traspuesta del producto:

• Una matriz es igual que su traspuesta si, y sólo si, es simétrica:

 El determinante de una matriz regular es igual al de su traspuesta:

Matriz Adjunta

Sea A una matriz de cuadrada de dimensión n

se define su matriz adjunta como:

donde A^{i , j} es la matriz que resulta al quitar la fila i y columna j a A.
Al elemento ad _{i , j} se le denomina ( i , j )- cofactor (o adjunto) de la matriz A.
Propiedades de la matriz adjunta:

• Adjunta de la identidad: 

• Adjunta de la traspuesta: 

• Adjunta del producto: 

• Si A es de dimensión n y k un escalar:

• Si A es regular, su inversa es:

Matriz Simétrica

Una matriz A cuadrada es simétrica si es igual a su traspuesta. Es decir,

Propiedades de las matrices simétricas

• La inversa de una matriz simétrica regular es simétrica.
• La adjunta de una simétrica es simétrica.
• La suma de simétricas es simétrica. El producto lo es si, y sólo si, también es conmutativo.
• Los autovalores (valores propios) de una matriz cuadrada, real y simétrica son reales.
• Autovectores (vectores propios) de autovalores distintos de una matriz cuadrada y real son ortogonales.
• Una matriz cuadrada y real, A, es simétrica si, y sólo si, es diagonalizable mediante una matriz de paso ortogonal, Q. Es decir,
  

 

Matriz Antisimétrica

Una matriz cuadrada A es antisimétrica si su traspuesta es igual a su opuesta, es decir, A^T = -A.

Matriz Definida Positiva

Una matriz A de dimensión m x n es definida positiva si para todo vector x = ( x₁ ,…, x_n) se cumple 

Si la desigualdad se cumple con el signo ≥ , diremos que es semi definida positiva.

Matriz (estrictamente) diagonalmente dominante por filas o columnas

Una matriz A de dimensión m x n es diagonalmente dominante por filas si 

diremos que los es por columnas si

Diremos que lo son estrictamente si la desigualdad se cumple de forma estricta.

Matriz Hessenberg

Una matriz cuadrada A de dimensión n > 1 diremos que es Hessenberg superior si todos los elementos por debajo de la diagonal -1 son nulos. Recordamos que la diagonal -k es la diagonal número k por debajo de la diagonal (principal).
Una matriz cuadrada A de dimensión n > 1 diremos que es Hessenberg inferior si todos los elementos por arriba de la diagonal -1 son nulos. Recordemos que la diagonal k es la diagonal número k por arriba de la diagonal (principal).

Hessenberg superior:

 

Hessenberg inferior: